SP#7: Unit Q Concept 2 Finding trig functions with one trig function and quadrant

Please see my SP7, made in collaboration with Jose Leal, by visiting their blog here.  Also be sure to check out the other awesome posts on their blog

WPP 13-14: Unit P Concets 6-7: Applications Of Law Of Sines & Cosines

Please see my WPP13-14, made in collaboration with Jose Leal, by visiting their blog here.  Also be sure to check out the other awesome posts on their blog here

BQ#1:Unit P Concepts 1 & 4: The Law of Sines AAS/ASA & Area of an Oblique Triangle

Law Of Sines AAS/ASA

1. We need the law of sines because sometimes we have to solve for triangles that are non right triangles. We can cut the triangle in half to form two triangles as shown in the picture below.

http://www.ck12.org/book/CK-12-PreCalculus-Concepts/r508/section/4.6/

and from the perpendicular line drawn from the two verticies we can find the other relationships as shown in the picture below. 

http://www.lhs.loganschools.org/~rweeks/trig/law_of_sines.jpg

Area Of An Oblique Triangle

The are of an oblique triangle is derived from A=1/2bh which is 1/2xBasexHeight. This relates to the area formula i am familiar with because we use sin of some angle for example sinB=h/a we multiply by "a" on both sides to get "h" alone and get h=1/2b(sinB) we substitute "h" for in the equation for "sinB" 

http://hotmath.com/hotmath_help/topics/law-of-sines.html

Resources

http://www.ck12.org/book/CK-12-PreCalculus-Concepts/r508/section/4.6/

http://hotmath.com/hotmath_help/topics/law-of-sines.html

http://www.lhs.loganschools.org/~rweeks/trig/law_of_sines.jpg

WPP# 12 Unit O Concept 10: Solving Angle Of Elevation & Depression Word Problems

Vanessa's Tootin' Train Express

A) The very cool express train is on the very coolest train track towards a super cool tunnel. The angle of elevation to the top of the super cool tunnel is 22°8'. If the base of the super cool tunnel is 848 feet from the very cool express train how high is the super cool tunnel?

Pickel Extravaganza

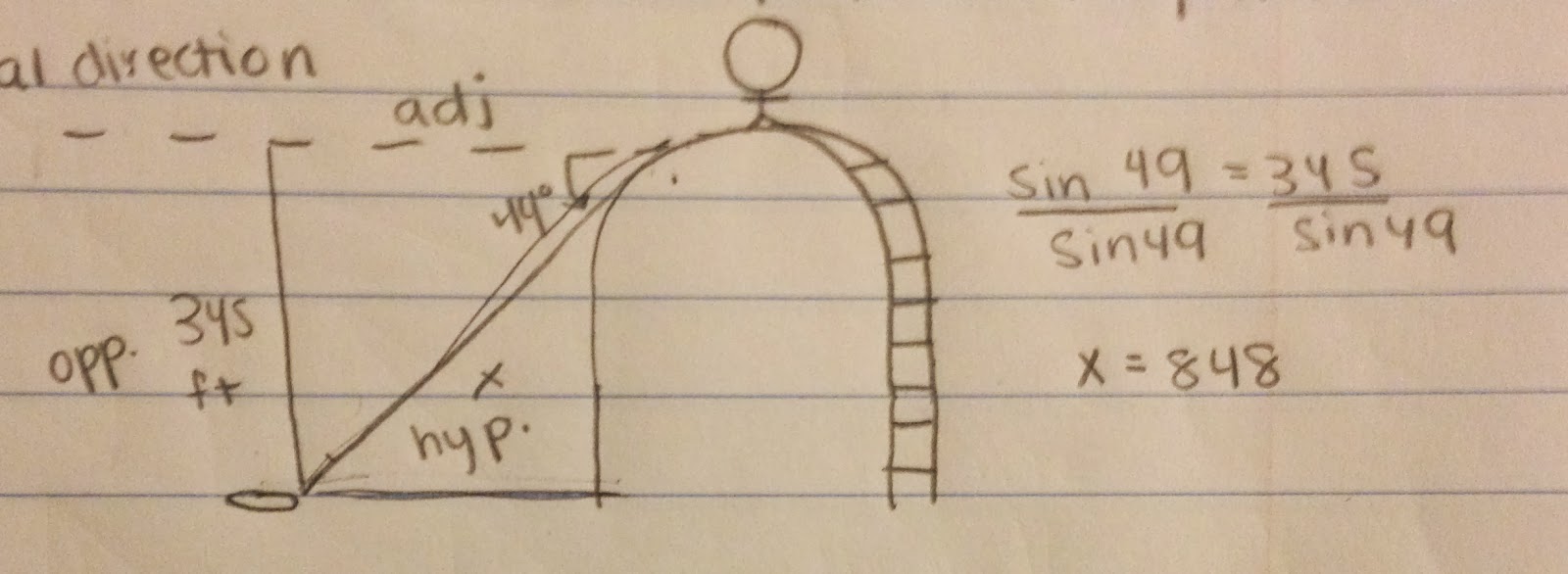
B) There is a man standing at the top of the Tunnel his name is Swanson Giggleton OH NO! He see's a pickle on the train track and doesn't want it to get squished. He measures the angle of elevation to the pickle to be 44°. He also knows that he is 345 feet from the ground. If there is a zip line that takes him in a diagonal direction straight to the pickle how long will it take him to reach the pickle & save the pickles life? 

I/D 2: Unit O-How can we derive the patterns for our special right triangles?

30-60-90

We label all the sides of the triangle 1. We then cut the triangle in half and notice that since all the angles are 60 the angle at the top will be cut in half and made into 30 degrees after this we can label the triangle sides "a", "b" and "c". The horizontal line was one and was cut in half so we know that the length of the new side is 1/2. We see that we are missing side "b" so we use the pythagorean theorem to solve for the missing angle. when we do a^2+b^2=c^2 we get "b" to equal radical (3/2) we know that we can't have any fractions so we multiply every side by two and get a=1 b=radical 3 c=2. we then can add the variable "n" to show that this pattern can be applied to another function.

45-45-90

i started by cutting the square diagonally. We know that each angle in the square is 90 degrees so by cutting it in half we know that half of 90 is 45 degrees. We also know that the two angles that are not the 90 degree angle are the same measurement. we are given 1 as the side length to all the sides and we label the sides "a", "b" and "c" we are missing "c" so we use the pythagorean theorem to find "c" we end up getting "c" to equal the square root of 2. We know that we can add the variable "n" to show that this also is a pattern that can be applied to another function.